Then how come I can't find the end of the packing tape?
-
Scam Alert. Members are reminded to NOT send money to buy anything. Don't buy things remote and have it shipped - go get it yourself, pay in person, and take your equipment with you. Scammers have burned people on this forum. Urgency, secrecy, excuses, selling for friend, newish members, FUD, are RED FLAGS. A video conference call is not adequate assurance. Face to face interactions are required. Please report suspicions to the forum admins. Stay Safe - anyone can get scammed.
Motion when locking the axis
- Thread starter Eyecon
- Start date
Dabbler
ersatz engineer
Then how come I can't find the end of the packing tape?
Clearly I'm not a toolmaker - I'm a hobbyist!
My mind is not structured like others are. I believe I can see these motions in my mind without the need for a model. When I was still doing automotive engineering, the guys used to routinely say that my brain was broken.
That said, I don't know how to use Fusion well enough to do what you two are doing. So maybe it's a good thing.
But maybe not too......
When you say that the screw is pivoting the Gibb, what do you mean? And about what axis? And how does that change the ability of the table to move?
Consider that there are a multitude of possibilities here:
The models are wrong
The movements are wrong
The constraints are wrong
My brain is wrong
The translation is wrong
I have no difficulty imagining a parallel but tapered Gibb that lifts at one end, the other end, or even at both ends. But I don't see how that allows the table to move any more or less than it did otherwise.
The only way for that to happen is with a Gibb that moves longitudinally. I don't think the Vertical movement at the screw translates into longitudinal movement.
On the other hand, I do see how a high spot might enable some bed play.
So I guess what I am trying to say is that I do not believe that the movement at the screw is consequential. It's a red herring.
It's better to set the movement at the screw aside for now and concentrate on figuring out what else could allow the bed to move.
Then how come I can't find the end of the packing tape?
That's your problem not mine. Your fingers are prolly too smooth. Gotta have some scars and roughness to be sensitive......
Edit - I'm mostly having fun with that statement. But quite seriously, I never have any trouble feeling the end of the thinnest packing tape we have ever used. And my wife makes it look ridiculously easy.
Last edited:
The CAD models are only meant to show that vertical movement of the gib on one end but not the other(like in my case) means that the gib is not making full contact on the dovetails on both sides (i.e. the mating surfaces are not coplanar). I think your statement is absolutely correct though(at least if I understood what you were saying): vertical movement of the gib on both ends is totally inconsequential, but any pivoting movement (the front lifts, the back drops for example) means that the 3 surfaces have an uneven gap between them (in my case possibly big gap between the dovetails and the gib in the front, but no gap in the back allowing the front screw to life the gib). Why does this matter? based on my understanding from the model, this uneven gap means that the saddle or table or whatever the gib is supposed to help slide can be wedged stuck not allowing for the surfaces to slide yet the setup can still wiggle side to side(this of course is the extreme case).
I think Stefan Gottswinter's technique shows it it best. In his video, he is checking for gib fit by checking this side to side wiggle/slop, the gib is wedged in a little and one end has no slop while the other does..meaning that if you screw the gib in you can bind the dovetails completely but can still move them side to side(at least on one end). This is very similar to what I observed: I have the gib in far enough to make the axial movement sticky yet I was still measuring side to side slop perpendicular to the direction of movement.
This is no different than what you already suggested as well, if there is dirt or a chip stuck between the gib and dovetail, the gib can be pushed in very tight against the dove tails but because of that chip, some part of the gib will not be making full contact with the dovetails allowing the adjusting screw to move it up or down and also causing side to side slop despite the gib being pushed far in(this up and down movement can be pivoting around that high spot caused by the chip or simply bending the gib like a flexible steel rule).
All of this is possible because the gib is not tall enough to be constrained up and down by the saddle and the ways. if it was constrained this way, it wouldn't move up or down even if it's not making perfect contact with the dovetails.
I hope I'm making sense
Last edited:
Actually, I think all three possibilities are inconsequential. The cos error for a long object like a Gibb is virtually nothing. So there is virtually no difference between a cocked (pivoted) Gibb and an uncocked one. To illustrate this, first consider a set of four parallels laying against each other. Either of the two middle ones can be put in any position without affecting the others, their relative position does not change no matter where you observe them.
Now consider four wedged parallels (tapered end to end in opposites). Again, the middle ones can be put in any position without affecting the others.
The Gibbs are the same except there are only two and the two dovetails makeup the other two parallels.
I agree that dirt or a high spot could do this. I just don't see how a parallel Gibb could.
Well, no. As I tried to show with parallels, the up and down movement does not allow any more or less movement than otherwise. It only means that the parallels are not stacked perfectly. It doesn't change their stack height. And it is the stack height that allows or prevents the table from having any play.
well I think that's exactly where the problem is, if the gib/dovtails were not tapered or the dove tails were just square ways this would be true. The compound angles formed by the front to back taper in combination with the dovetail angle makes this impossible as the CAD model shows.
Let's consider another easy example: think of the gib/non sliding dovetail pair as an adjustable parallel. If you put an adjustable parallel between two 123 blocks and squeeze all three together on a surface plate, you can rotate the adjustable parallel between those two 123 block and the blocks would still sit flat on the surface plate. If those the vertical sides of 123 blocks and the adjustable parallel to the surface plate were cut at any angle other than 90 deg (that is still relative to the surface plate), you wouldn't be able to do that without pushing one of the 123 blocks off the plate. That's basically what the CAD model shows.
I'll mock this up using some wooden blocks, it was very counter intuitive for me at least and that's exactly why I decided it to try in CAD
Last edited:
I'm not quite sure if this sequence will show the resultant dimensional differences properly but here goes. Remember my example is just made up dimensions, not the physical assembly
This shows the simplified table/gib model like my little movie. Blue stationary center section. Green gib mated to dovetail surface. Both are 60-deg angles. I omit the opposing table to the right of gib because I'm just looking for resultant dimensions on the thick end, Plane1
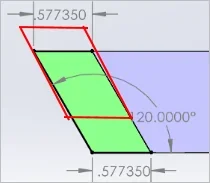
This shows the base case reference dimensions on the thick end. Top & bottom dimensions. The gib included angle is 60-deg so we get 120.000 deg angle between horizontal & gib surface. All as we would expect.
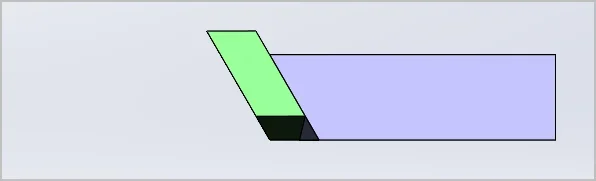
Now we cock the gib strip up. This can be a more complicated combined motion, but just for this example, I left the axial position of the gib the same, rotate gib about lower edge of small end & constrain the mate between dovetail surfaces so they can slide. The bottom gib surface is inclined 2-deg for reference.
Now take new measurements relative to same plane. The gib has now pushed out to 0.578709 at the top of blue surface, so subtract original 0.577350 = 0.0014" difference
Note the angle of the outboard gib surface is now greater than 120.0 deg vs horizontal so it cannot match the opposing casting dovetail plane. It would be a point contact with a wedge gap.
This shows the simplified table/gib model like my little movie. Blue stationary center section. Green gib mated to dovetail surface. Both are 60-deg angles. I omit the opposing table to the right of gib because I'm just looking for resultant dimensions on the thick end, Plane1
This shows the base case reference dimensions on the thick end. Top & bottom dimensions. The gib included angle is 60-deg so we get 120.000 deg angle between horizontal & gib surface. All as we would expect.
Now we cock the gib strip up. This can be a more complicated combined motion, but just for this example, I left the axial position of the gib the same, rotate gib about lower edge of small end & constrain the mate between dovetail surfaces so they can slide. The bottom gib surface is inclined 2-deg for reference.
Now take new measurements relative to same plane. The gib has now pushed out to 0.578709 at the top of blue surface, so subtract original 0.577350 = 0.0014" difference
Note the angle of the outboard gib surface is now greater than 120.0 deg vs horizontal so it cannot match the opposing casting dovetail plane. It would be a point contact with a wedge gap.
@PeterT awesome illustration! so not only is the front of the gib .0014" wider than the back, it would also be only making contact on the top edge of the opposing dovetail, all this can introduce side to side slop in the mechanism! And that's with the assumption that the surface are flat and matching in angle!
Former Member
Guest
Its clearly more than 3/10s so of course you can't find it silly boy.....Then how come I can't find the end of the packing tape?
Former Member
Guest
I think you may be in to something here. My gibs can also lift but I have none of the issues.The CAD models are only meant to show that vertical movement of the gib on one end but not the other(like in my case) means that the gib is not making full contact on the dovetails on both sides (i.e. the mating surfaces are not coplanar). I think your statement is absolutely correct though(at least if I understood what you were saying): vertical movement of the gib on both ends is totally inconsequential, but any pivoting movement (the front lifts, the back drops for example) means that the 3 surfaces have an uneven gap between them (in my case possibly big gap between the dovetails and the gib in the front, but no gap in the back allowing the front screw to life the gib). Why does this matter? based on my understanding from the model, this uneven gap means that the saddle or table or whatever the gib is supposed to help slide can be wedged stuck not allowing for the surfaces to slide yet the setup can still wiggle side to side(this of course is the extreme case).
I think Stefan Gottswinter's technique shows it it best. In his video, he is checking for gib fit by checking this side to side wiggle/slop, the gib is wedged in a little and one end has no slop while the other does..meaning that if you screw the gib in you can bind the dovetails completely but can still move them side to side(at least on one end). This is very similar to what I observed: I have the gib in far enough to make the axial movement sticky yet I was still measuring side to side slop perpendicular to the direction of movement.
This is no different than what you already suggested as well, if there is dirt or a chip stuck between the gib and dovetail, the gib can be pushed in very tight against the dove tails but because of that chip, some part of the gib will not be making full contact with the dovetails allowing the adjusting screw to move it up or down and also causing side to side slop despite the gib being pushed far in(this up and down movement can be pivoting around that high spot caused by the chip or simply bending the gib like a flexible steel rule).
All of this is possible because the gib is not tall enough to be constrained up and down by the saddle and the ways. if it was constrained this way, it wouldn't move up or down even if it's not making perfect contact with the dovetails.
I hope I'm making sense
The dovetails may be different angles from from one part to the next which will definitely cause issues.
The taper from the base and gib are different (lengthwise) which will definitely cause binding and slop at the same tome as one end is tight and the other loose and you can never achieve a proper bearing surface fit.
So this is where we disagree.
Unless of course my mind is broken. Which is highly likely since at least two of you see it differently than I do.
You don't lift the Gibb about the lower edge of of the small end. You lift it about an axis that is 90 degrees to the long axis of the cross section.
The fact that the Gibb is a parrallogram is an artifact of the need to install it in the dovetail. It doesn't constrain the motion until the Gibb reaches the extremes of the enclosure. That's why it can raise a bit as you tighten the screw. But until then, it's just a plate sliding between two parallel surfaces.
Yes, the two parallel surfaces do diverge (or converge) as the rotation proceeds, but only as the cosine of the angle becomes significant. At small angles its virtually zero.
We can test this by compressing the plate, removing the screw, and lifting the plate manually with a small screwdriver. The force required will not change as it is lifted if I am correct. But if you are correct it will get progressively more difficult as the Gibb lifts.
Fundamentally, the Gibb does not lift in a vertical plane about that far bottom edge. It is constrained by the angle of the dovetail and the matching Gibb which are the same. So the Gibb rotates about an axis that is 90 degrees to the planes of the dovetail constraints. It rotates until it hits another constraint which is the top of the Gibb channel.
Your machine is already apart.
Remove and mark the two gibbs so you can put them back where they belong.
Lay them on top of each other on a flat surface - a surface plate if you have one. Measure the stack height at one end. Then rotate the Gibbs at that end away from each other (like a pair of scissors) by a quarter inch or so (way more than the 16th inch you get with the screw as installed). Now measure the stack height again. It won't be any different.
Of course, that whole concept goes out the window if the Gibbs flats are not parallel. But you confirmed that they were when I pushed that question back at the beginning of this thread. Mine with this same behaviour are parallel. Mine DO NOT produce the bed play that you have.
I remain convinced that your models do not accurately reflect the real situation and that the lifting is unrelated to the bed play. I do believe that a high spot or some dirt in the center of the Gibbs might cause this.
But I can't wait to see all your measurements. They might tell a different story.
I think there is a problem with the model (I presume the dimensions were computer generated?):
If the gib moves up the side of the dove tail (blue surface) and the gib is a true parallelogram (in cross section) at any give point along its length, then the 120* angle would remain at 120* no matter how high the gib end is lifted off the reference surface.
The lifting does however tighten up any space between the two parallel dove tail surfaces (only one is shown in you model) as seen by the dimension change at the top.
Also, as the end of the gib lifts because the adjusting screw is tightened, not only does the thread pitch of the adjuster push the gib in axially, but also the changing contact angle between the screw head and the face of the gib acts in the same direction, pushing the gib deeper.
These errors may in fact be small - especially since the gib seems to have side to side play even after the axial motion of the saddle has been locked up due to the depth of the gib.
Thus, I would conclude (as has been pointed out by others), there must be some taper angle mismatch, a raised burr, or some other mechanical debris at play.
We agree. If both ends if the gib displace the same amount vertically (from black position to red position) then there is no net effect of pushing laterally to the side onto orange surface. And yes, the angle remains at 120-deg. But this only exists by defining that exact constraint: the same amount vertically on both ends. The purpose of my sketch was to evaluate what happens if one end stays low & other goes high. I'm not saying if or how or probability, its just a what-if exercise.
You are free to postulate whatever constraints you prefer, evaluate them accordingly & ignore any others. You saw his video where the gib cocked up within the gap headroom when he turned the adjuster screw right? Did you see the opposite end move up the exact same amount simultaneously at the exact same time? No, neither did I. The absence of seeing something occur doesn't mean it did not occur or could not occur. Is just convenient spot to fill in your own theory.
So I wondered out loud if one gib end had large headroom gap allowance & the opposing gib end had low gap allowance, this could be a combination whereby the gap end could rise independent & disproportionate to the other. Pivoting on the bottom edge/point of the low gap end is easier to model & 'legal' from a constraint standpoint, otherwise the program would complain. The rest of the exercise is just showing that there is a lateral displacement consequence as indicated by resultant before & after dimensions. This possible effect was not intuitive, at least to me. I thought I was careful to define the assumptions but apparently not. Now is the probability of this occurring high or low or something in between? I dunno. I am now more convinced that the dimensional amount is very low, but I only know that by seeing numbers. There is more to unpack to this story when we see more parts & measurements.
Attachments
Jez Peter. I hope you are not as fed up with me as that sounds. I'm just debating your models, and trying my best to explain what I see, not calling anyone out. If I come across otherwise then I am sincerely sorry for that.
What I see in my head does not require both ends to lift simultaneously. But they could, and it wouldn't make any difference one way or the other.
FWIW, I am totally open to changing my mind when/if I'm shown something that causes me to realize my mistake. For the time being, I'm pretty sure about what my mind sees. Hence the challenges to your model. Please don't take personal offense, none was intended.
It was just a cad/geometry/math puzzle mostly for my own curiosity. I also had a gut feel that any differential lift between gib ends would result in miniscule lateral dovetail gap difference practically speaking. Why? Because of the overall boundary conditions. A) the top view included angle of a gib is very shallow to begin with, so any vertical displacement/rotation component of the gib is an even smaller subset.
B) even with say 0.2" available top gap one end, the gib cant rotate very far before it hits the underside of table. So it wont be much at all. Does it amount to a thou, a tenth, a millionth? I dunno. I have the tools so why not find out. The point is I also had a sense of 3D geometry that it was not zero. One more try with pictures...
The green gib is tapered in top view. If it displaced axially along the dovetail (up & down in this particular orientation) it means more or less gap between pink & blue blocks. The purpose of the gib, right?
An equivalent way to look at it (for more convenient measurement purposes) is fix the blue block & allow the pink block to slide laterally until it mates the gib dovetail angle.
Now if I move the gib axially (up/down) the pink block moves left right in black arrow direction & I can measure more readily.
Looking on end, even though the gib is a tapered, if it were displaced along the dovetail angle (black arrow) there would be no resultant side effect seen by the pink block. I think we all agree, butthat wasnt the point of the excercise
This was the point of exercise. Now we cock the gib slightly like so. By cock I mean it is again in full contact with the blue block dovetail, but it is rotating or pivoting on the lower left edge. Don't ask yourself how or why for the moment, just drink the Koolaid. It does not violate any geometric mating, it is a legal orientation. Its just a hypothetical what-if.
Now we look at it obliquely on end again. Here you have to visualize the pink block is on the left trying to make contact with the gib.
Same question, will the pink block move as a result of this gib orientation? Is it zero (stationary)? Or is it a little bit?
What about now. Its the exact same displacement mode, just more of it
End view, the gib now occurs noticeably to the left. Of course this is nonsense because its completely outside the boundary conditions
which is why I took measurements from the the same reference positions, from the corner of blue block, horizontally left to the intersection of the gib left surface, wherever that ends up.
If they are different, which they are, then the pink block would have to be in a slightly different position. At least that's my conclusion to this point.
B) even with say 0.2" available top gap one end, the gib cant rotate very far before it hits the underside of table. So it wont be much at all. Does it amount to a thou, a tenth, a millionth? I dunno. I have the tools so why not find out. The point is I also had a sense of 3D geometry that it was not zero. One more try with pictures...
The green gib is tapered in top view. If it displaced axially along the dovetail (up & down in this particular orientation) it means more or less gap between pink & blue blocks. The purpose of the gib, right?
An equivalent way to look at it (for more convenient measurement purposes) is fix the blue block & allow the pink block to slide laterally until it mates the gib dovetail angle.
Now if I move the gib axially (up/down) the pink block moves left right in black arrow direction & I can measure more readily.
Looking on end, even though the gib is a tapered, if it were displaced along the dovetail angle (black arrow) there would be no resultant side effect seen by the pink block. I think we all agree, butthat wasnt the point of the excercise
This was the point of exercise. Now we cock the gib slightly like so. By cock I mean it is again in full contact with the blue block dovetail, but it is rotating or pivoting on the lower left edge. Don't ask yourself how or why for the moment, just drink the Koolaid. It does not violate any geometric mating, it is a legal orientation. Its just a hypothetical what-if.
Now we look at it obliquely on end again. Here you have to visualize the pink block is on the left trying to make contact with the gib.
Same question, will the pink block move as a result of this gib orientation? Is it zero (stationary)? Or is it a little bit?
What about now. Its the exact same displacement mode, just more of it
End view, the gib now occurs noticeably to the left. Of course this is nonsense because its completely outside the boundary conditions
which is why I took measurements from the the same reference positions, from the corner of blue block, horizontally left to the intersection of the gib left surface, wherever that ends up.
If they are different, which they are, then the pink block would have to be in a slightly different position. At least that's my conclusion to this point.
Attachments
Last edited:
...cntd...
If I position the pink block with a small but open gap near the bottom edge
then I look at the upper corner of pink block, it is inside/interfering the gib area. Confirmation that the 2 surfaces are not planar. So the corner of the pink block would be making point contact with the gib
THE END lol
If I position the pink block with a small but open gap near the bottom edge
then I look at the upper corner of pink block, it is inside/interfering the gib area. Confirmation that the 2 surfaces are not planar. So the corner of the pink block would be making point contact with the gib
THE END lol
@PeterT thank you for taking the time to explain this and also to make measurements. My initial setup while very crude served to confirm the same: a lifted tapered gib that’s making full contact with one of the dovetails cannot make full contact with the other dovetail. Why does this matter? A gib that doesn’t not make full contact can act as a wedge that hinders the sliding movement while still allowing for side to side slop. At this point it doesn’t really matter why it’s not making full contact(a chip, wrong geometry, or it’s simply not seated flat because it’s not tall enough…) bottom line is this behaviour can explain what I observed on the mill: a stiff axial movement along the dovetails with less than ideal rigidity side to side perpendicular to the dovetails.
How to correct this in my case(clean, shim the gib, or modify it’s geometry) will ultimately depend on what I find out when I take the mill apart and methodically take measurements that will hopefully confirm what the problem is.
Thanks again to everyone for trying to think this through with me. Once I get the chance to disassemble everything I’ll report back on my findings.
How to correct this in my case(clean, shim the gib, or modify it’s geometry) will ultimately depend on what I find out when I take the mill apart and methodically take measurements that will hopefully confirm what the problem is.
Thanks again to everyone for trying to think this through with me. Once I get the chance to disassemble everything I’ll report back on my findings.