Little bit of shop time

[thriller007]

Couple more small projects. First is a two sided high speed steel holding device for grinding tools while keeping my fingers away. Ended up going into the old sockets box and sacrificing a 3/8” and a 1/4” socket. Cut off the square part and pressed into the aluminum and then drilled and tapped for tightening screws.

Next was just a simple countersink bit holding device. Found out on that one I need to make or buy a different knurling tool since mine is not the clamp style and just relays on pressure and has to be perfectly set up. What do you use for knurling?

 

[thriller007]

Ok things are getting a bit more complex. The bump style knurler I have needs to really be pressed hard against the workpiece so I am trying to make a different clamp style that still uses the original tool parts.

 

[DavidR8]

Couple more small projects. First is a two sided high speed steel holding device for grinding tools while keeping my fingers away. Ended up going into the old sockets box and sacrificing a 3/8” and a 1/4” socket. Cut off the square part and pressed into the aluminum and then drilled and tapped for tightening screws.

Next was just a simple countersink bit holding device. Found out on that one I need to make or buy a different knurling tool since mine is not the clamp style and just relays on pressure and has to be perfectly set up. What do you use for knurling?

I have all the bits and pieces necessary to build the straddle type knurler that @Mikey has shown on his project page.
Project #62 on the to do list.
Edit: sorry I referenced a member project on Hobby-Machinist.con

 

[PeterT]

There are quite a few plans on the internet for clamp/scissor type knurlers that you can suit to your toolpost & lathe dimensions. You can use your knurling wheels, assuming they are decent quality & good shape. Some things to consider
- maximum diameter you intend to knurl (affects your frame size)
- hardened axles, either your own or commercial dowel pins, There is a lot of pressure imparted on them & kind of dirty environment. Also have a easy & reliable means to remove the axles, maybe like set screw flat through the frame. Some spendy knurlers have axles pressed in the frame which I suppose prevents them from spinning but are a royal PITA to change wheels which is something you probably want to do often
- tensioning mechanism: most designs have a nut or bolt head, but vary in how they apply force. Consider how you will apply progressive force & meanwhile keep the tool/wrench/your hand out of the way which can be quite close to the ouchy spinny parts
- use decent knurl wheels. These are kind of like taps & dies & other tools, crappy ones just don't work as well
- turn the part OD according to the simple formula before knurling (OD is a function of the wheel pitch). A lot of guys skip this step which is why they have hit & miss results. Think of it kind of like gears meshing properly

 

[DavidR8]

Joe Pi has an excellent video on knurling.

 

[Tom Kitta]

I got excellent result knurling on my smaller lathe when I did feed of about 0.007 and I moved back and forth using the screw locked - after 4 passes I got nice deep cut that was perfectly even. I.e. I moved forward, back, forward, back. Each time I made sure there is lots of pressure.

Also I finally got the thing to part while on power feed.

Joe is quite good at what he does - for a Pole with a last name "baker".

 

[thriller007]

Joe Pi has an excellent video on knurling.

Thanks for the heads up on that video. I just watched it. Here it is for anyone else.

I always thought that the circumference of the wheel would have a great effect on how the knurl turned out and that was confirmed. (thanks as well @PeterT for pointing that out as well above.) Other than measuring how many TPI my knurls have by using the non-accurate way of using a flexible tape to wrap around how do I figure that out? Should there be some sort of markings on them?

 

[DavidR8]

Thanks for the heads up on that video. I just watched it. Here it is for anyone else.

I always thought that the circumference of the wheel would have a great effect on how the knurl turned out and that was confirmed. (thanks as well @PeterT for pointing that out as well above.) Other than measuring how many TPI my knurls have by using the non-accurate way of using a flexible tape to wrap around how do I figure that out? Should there be some sort of markings on them?

Wouldn’t micing them and converting that number to circumference work to give you the “I” of TPI?

 

[Janger]

Knurl a piece of a paper and measure the marks.

 

[PeterT]

If your wheels don't have ID markings then its kind of like a mystery gear, you'll have to measure OD & count teeth. The potential problem is where did the wheel come from? Maybe its a 15mm wheel from Asia/Europe, not a 5/8" wheel from N-Am.

Joe has some good information & a ton of machining experience. But I had to watch his math explanation a few times. I'm a bit confused. I think he is saying:
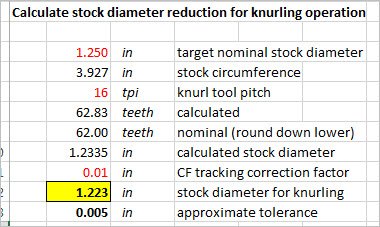
- calculate the nominal part circumference C = Dia * Pi C = 1.25 in * 3.14159 = 3.927 in
- calculate equivalent number teeth N = C / circumference N = 3.927 * 16 TPI (same as 1/16=0.0625) N = 62.83
- N is not a round number because of the 0.83 remainder, so the knurl wheels wont track the shaft OD, we all agree

Around here I lose the scent. His whiteboard says a reduced diameter of 1.243 inch yields an even 63 teeth? But plugging those numbers into his same formula gets...
C = Dia * Pi C = 1.243 in * 3.14159 = 3.905 in
N = C / circumference N = 3.905 * 16 TPI = 62.479 teeth So we still have a remainder problem, this time 0.47. Its smaller but still not a round number
I looked in the comments & nobody mentioned this. Am I missing something here? Maybe he slipped a digit. He mentions 7 thou?

He could have just rearranged the formula a bit & calculated directly: Dia = N / (P * pi)
if N = 62, resultant Dia = 1.233 in (this is the best way because it calculates closest shaft diameter under nominal)
if N = 63, resultant Dia = 1.253 in (it works but note is bigger diameter than original nominal shaft size)

I used this link to make a little spreadsheet. They mention other correction factors over & above this pitch calculation. They also quantify a +/- tolerance which is (IMO) why sometimes knurling appears to work better than other times.
https://accu-trak.com/technicalinfo/blank_diameter_selection.html

 

[DavidR8]

You’ll also notice that even when he turned down the shaft to the diameter where the knurls should have single tracked they still multi tracked.
My takeaway was to just press on and knurl.

 

[PeterT]

Knurling is a black art because there are so many interconnecting variables and technique. Its a material forming/deformation process, not a cutting/removal process. Most people (me included) just want a pretty pattern that doesn't visually suck & provide a surface we can grip our fingers on. But when you see well made knurls under magnification, especially tough materials like tool steel on gun parts, or delicate materials like camera parts, makes you appreciate where the bar is set.

Back to Joe.P tracking (I noticed that too) I included the diameter with +/- tolerance using same website info. This shows the allowable range even with the factors accounted for. But that is for one specific diameter/knurl combination. I think this is the root of the issue. People get good results on a knurl & conclude the math doesn't matter. But next one slightly different size looks like crap so its a mystery or they chock it up to other things. I think its just the combination of diameter & pitch lands you inside or outsize the recommended range. So IMO its worth doing the calculation especially if its easy to plunk in spreadsheet. I mean you need turn the OD to some value anyways, may as well give yourself best chance of success.

 

[RobinHood]

Yes, his board is wrong. He says that “if you take 7thou off the diameter....” which is 1.243” - that is what he has written. BUT, if you have 63 teeth, the ideal diameter is 1.253” as you mention Peter.

So if you have a 63 tooth wheel and used it on a nominal 1 1/4” shaft (they are usually oversized) you probably still get better results than using a 62 tooth wheel on a 1 1/4” nominal shaft turned down to 1.243.

He does mention a very important factor: the initial bite needs to be almost to final depth for a successful knurl. No sneaking up on things.

I have a scissor type tool (and a swivel head and a straight one). I prefer the scissor one. I touch off so that both upper and lower wheels are well engaged, but don’t leave marks. I note the cross slide position. I back the tool off to clear the part and tighten the scissors by a 1/4 to 1/2 turn. Then run the lathe at very low speed, feed in to the same cross slide number. Lots of lube. The knurl is well formed after maybe 5 revs of the part. Then I just let it “spark” out - listen for the sound to change from a well loaded tool running to one that is lightly loaded. And you are done. It really moves a lot of metal.

Pays to do a sample first. Adjust clamp pressure, OD, speed, lube, etc. as required. The knurling rollers need to be spotless before you start. Any plugged up grooves will show. That’s another reason why you don’t dwell on the part: if there are tiny bits that come off, they will clog the rollers and you can just watch the (once) beautiful knurling get destroyed in a few turns of the part.

 

[thriller007]

G

Knurl a piece of a paper and measure the marks.

Yes that worked good and it was 16 tpi